자본자산가격결정모형 (CAPM)

자본자산가격결정모형(capital asset pricing model, CAPM) 

개별증권을 비롯한 모든 자본자산의 적합한 위험(체계적 위험)과 기대수익률 사이에 존재하는 균형관계를 설명하는 모형


체계적 위험 & 비체계적 위험

다음 그래프는 포트폴리오에서 구성자산 수가 많아질수록 제거할 수 없는 위험인 체계적인 위험만 남게됨을 의미한다.

체계적 위험은 시장 전체적인 위험(거시경제변수같은...)으로 제거할 수 없는 위험을 의미하고, 비체계적인 위험은 포트폴리오에서 구성자산을 다양화 함으로써 제거할 수 있는 위험을 의미한다. 투자자가 포트폴리오를 구성하는 이유가 일정한 기대수익률하에서 투자위험을 최소화시키기 위한 위험분산효과를 노리는 것임을 상기하면 된다.


증권시장선(security market line, SML)

모든 위험자산의 체계적 위험(아래 수식의 베타계수)과 기대수익률의 선형관계를 나타내는 직선식을 자본자산가격결정모형(CAPM) 또는 증권시장선이라 한다. CAPM과 SML은 보통 같은 의미로 사용하지만 엄밀히 구분하면 CAPM은 다음 수식을 의미하며, SML은 CAPM의 수식을 그래프로 나타낸 것이다.

 

: 자산 j의 기대수익률
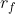: 무위험 이자율
: 시장포트폴리오의 기대수익률
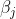: 시장수익률의 변동에 대한 개별주식의 민감도

위의 수식에서 베타계수()가 큰 증권일수록 시장수익률의 변동에 대해 보다 민감하게 반응한다고 하며
-  > 1.0 이면 공격적 주식(aggressive stock)
-  < 1.0 이면 방어적 주식(defensive stock)이라고 한다.


증권시장선 그래프는 다음과 같다.

문제-1) 증권시장선과 기대수익률
무위험이자율이 8%이며, 시장수익률이 10%로 기대될 때...
 
(1) 증권시장선을 구하라



 



(2) 베타가 1.5인 증권 k의 기대수익률을 구하라



 



 


문제-2) CAPM에 의한 자산 평가
A기업의 기말 주식가격은 20,000원으로 기대되며 이 주식의 베타계수는 1.5이다. 또한 시장의 기대수익률은 12%이며, 무위험이자율은 8%이다. A기업의 현재 주식가치는 얼마인가? (단, 배당은 없다고 가정한다.)

   (각괄호 안에는 증권시장선 공식)